adj. (Mécanique) se dit de ce qui a rapport à un centre. Voyez CENTRE.

C'est ainsi que nous disons éclipse centrale, feu central, force centrale, règle centrale, etc. Voyez les articles FEU, ÉCLIPSE, etc.

Forces centrales, sont des forces ou puissances par lesquelles un corps mu tend vers un centre de mouvement, ou s'en éloigne.

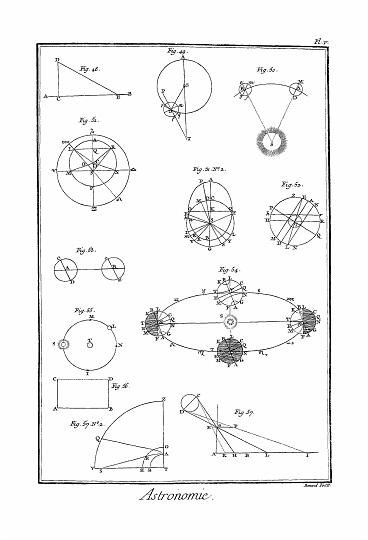
C'est une loi générale de la nature, que tout corps tend à se mouvoir en ligne droite ; par conséquent un corps qui se meut sur une ligne courbe, tend à chaque instant à s'échapper par la tangente de cette courbe : ainsi pour l'empêcher de s'échapper suivant cette tangente, il faut nécessairement une force qui l'en détourne et qui le retienne sur la courbe. Or c'est cette force qu'on appelle force centrale. Par exemple un corps A (fig. 24. Mécan.) qui se meut sur le cercle B E A, tend à se mouvoir au point A suivant la tangente A G, et il se mouvrait effectivement suivant cette tangente, s'il n'avait pas une force centrale qui le pousse vers le point C, et qui lui ferait parcourir la ligne A M dans le même temps qu'il parcourait A D ; de sorte qu'il décrit la petite portion de courbe A E.

Remarquez qu'il n'est pas nécessaire que la force centrale soit toujours dirigée vers un même point : elle peut changer de direction à chaque instant, il suffit que sa direction soit différente de celle de la tangente, pour qu'elle oblige le corps à décrire une courbe. Voyez CENTRE DE MOUVEMENT ; voyez aussi FORCE.

Les forces centrales se divisent en deux espèces, eu égard aux différentes manières dont elles sont dirigées par rapport au centre, savoir en centripetes et en centrifuges. Voyez ces mots.

Lais des forces centrales. Le célèbre M. Huygens est le premier qui ait découvert ces lais. Mais outre qu'il les a données sans démonstration, il ne s'est appliqué qu'à déterminer les lois des forces centrales dans le cas où le corps décrit un cercle. Plusieurs auteurs ont démontré depuis les lois données par M. Huygens, et le célèbre M. Newton a étendu la théorie des forces centrales à toutes les courbes possibles.

Parmi les auteurs qui ont démontré les propositions de M. Huygens, personne ne l'a fait plus clairement et d'une manière plus simple, que le marquis de l'Hôpital dans les mémoires de l'académie de 1701. 1°. Il commence par enseigner la manière de comparer la force centrale avec la pesanteur ; et il donne là-dessus la règle générale suivante, qui renferme toute la théorie des forces centrales.

Supposons qu'un corps d'un poids déterminé se meuve uniformément autour d'un centre avec une certaine vitesse, il faudra trouver de quelle hauteur il devrait être tombé pour acquérir cette vitesse ; après quoi on fera cette proposition : comme le rayon du cercle que le corps décrit est au double de cette hauteur, ainsi son poids est à sa force centrifuge. Il est visible que par cette proposition on peut toujours trouver le rapport de la force centrale d'un corps à son poids ; et que par conséquent on pourra facilement comparer les forces centrales entre elles. Mais si on veut se contenter de comparer les forces centrales entre elles sans les comparer avec la pesanteur, on peut se servir de ce théorème, que les forces centrales de deux corps sont entre elles comme les produits de leurs masses multipliés par les carrés de leurs vitesses, et divisés par les rayons ou par les diamètres des cercles qu'ils décrivent. On peut démontrer cette proposition sans calcul, d'après M. Newton, de la manière suivante. Imaginons les cercles que ces corps décrivent comme des polygones réguliers semblables, d'une infinité de côtés ; il est certain que les forces avec lesquelles chacun des corps frappe un des angles de ces polygones, sont comme des produits de leurs masses par leurs vitesses. Or dans un même temps ils rencontrent d'autant plus d'angles qu'ils vont plus vite, et que le cercle est d'un rayon plus petit : donc le nombre des coups dans un même temps, est comme la vitesse divisée par le rayon, donc le produit du nombre des coups par un seul coup, c'est-à-dire la force centrale, sera comme le produit de la masse multiplié par le carré de la vitesse, et divisé par le rayon.

Donc si deux corps M, m, décrivent les circonférences du cercle C, c avec des vitesses V, u pendant les temps T, t, et que les forces centrales de ces corps soient F, f, et les rayons des cercles qu'ils décrivent R, r, on aura F : f : : (M x V V)/R : (m u u)/r ; de plus, on a V : u : : C/T : c/t : : R/T : r/t ; donc on aura encore F : f : : MR/TT : (m r)/(t t).

2°. Il est aisé de conclure de-là, que si deux corps de poids égal décrivent des circonférences de cercles inégaux dans des temps égaux, leurs forces centrales seront comme les diamètres A B et H L (Planc. de Mécan. fig. 24.) car si m = M et t = T, on aura F : f : : R : r ; et par conséquent si les forces centrales de deux corps qui décrivent des circonférences de deux cercles inégaux, sont comme leurs diamètres, ces corps feront leurs révolutions dans des temps égaux.

3°. La force centrale d'un corps qui se meut dans une circonférence de cercle, est comme le carré de l'arc infiniment petit A E, divisé par le diamètre A B ; car cet arc infiniment petit décrit dans un instant, peut représenter la vitesse, puisqu'il lui est proportionnel. Ainsi puisqu'un corps décrit dans des temps égaux, par un mouvement uniforme, des arcs égaux A E, la force centrale par laquelle le corps est poussé dans la circonférence du cercle, doit être constamment la même.

4°. Si deux corps décrivent par un mouvement uniforme différentes circonférences, leurs forces centrales seront en raison composée de la doublée de leur vitesse, et de la réciproque de leur diamètre ; d'où il s'ensuit que si les vitesses sont égales, les forces centrales seront réciproquement comme les diamètres ; et si les diamètres A B et H L sont égaux, c'est-à-dire si les mobiles se meuvent dans la même circonférence, mais avec des vitesses inégales, les forces centrales seront en raison doublée des vitesses.

Si les forces centrales de deux corps qui se meuvent dans des circonférences différentes, sont égales, les diamètres A B et H L seront en raison doublée des vitesses.

5°. Si deux corps qui se meuvent dans des circonférences inégales sont animés par des forces centrales égales, le temps employé à parcourir la plus grande circonférence sera au temps employé à parcourir la plus petite, en raison soudoublée du plus grand diamètre A B, au moindre H L : c'est pourquoi on aura T2 : t2 : : D : d ; c'est-à-dire que les diamètres des cercles dans les circonférences desquels ces corps sont emportés par une même force centrale, sont en raison doublée des temps.

Il s'ensuit aussi de là, que le temps que des corps poussés par des forces centrales égales emploient à parcourir des circonférences inégales, sont proportionnels à leurs vitesses.

Les forces centrales sont en raison composée de la directe des diamètres et de la réciproque des carrés des temps employés à parcourir les circonférences entières.

6°. Si les temps dans lesquels les corps parcourent les circonférences entières ou des arcs semblables, sont comme les diamètres des cercles, les forces centrales seront alors réciproquement comme ces mêmes diamètres.

7°. Si un corps se meut uniformément dans la circonférence d'un cercle avec la vitesse qu'il acquiert en tombant de la hauteur A F, nous avons dit que la force centrale sera à la gravité comme le double de la hauteur A F est au rayon C A ; et par conséquent si on nomme G la gravité du corps, la force centrifuge sera (2 A F x G)/(C A). Par-là on connaitra quelle doit être la force centrifuge et la vitesse d'un corps attaché à un fil, pour qu'il ne rompe point ce fil en circulant horizontalement : car supposons qu'un poids de trois livres, par exemple, rompe le fil, et que le poids du corps soit de deux livres, on aura G égal à deux livres, et (2 A F x 2)/(C A) devra être plus petit que trois livres, d'où l'on tire A F < (3 C A)/4 : ainsi la vitesse que le corps doit avoir pour ne point rompre le fil, doit être plus petite que celle qu'il acquerrait en tombant d'une hauteur égale aux 3/4 du rayon. Si le corps circulait verticalement, il faudrait que (2 A F x G)/(C A) + G fût < trois livres.

8°. Si un corps grave se meut uniformément dans la circonférence d'un cercle, et avec la vitesse qu'il peut acquérir en tombant d'une hauteur égale à la moitié du rayon : la force centrale sera alors égale à la gravité ; réciproquement si la force centrale est égale à la gravité, le corps se mouvra dans la circonférence du cercle avec la même vitesse qu'il aurait acquise en tombant d'une hauteur égale à la moitié du rayon.

9°. Si la force centrale est égale à la gravité, le temps qu'elle emploiera à faire parcourir la circonférence entière, sera au temps dans lequel un corps grave tomberait de la moitié du rayon, comme la circonférence est au rayon.

10°. Si deux corps se meuvent dans des circonférences inégales et avec des vitesses inégales, de sorte que les vitesses soient entr'elles en raison réciproque de la soudoublée des diamètres, les forces centrales seront en raison réciproque de la doublée des distances au centre des forces.

11°. Si deux corps se meuvent dans des circonférences inégales avec des vitesses qui soient entr'elles réciproquement comme les diamètres, les forces centrales seront en raison inverse des cubes de leur distance au centre des forces.

12°. Si les vitesses de deux corps qui se meuvent dans des circonférences inégales, sont en raison inverse de la soudoublée des diamètres, les temps qu'ils emploieront à faire leur révolution entière ou à parcourir des arcs semblables, seront en raison inverse de la triplée des distances du centre des forces : c'est pourquoi si les forces centrales sont en raison inverse de la doublée des distances du centre, les temps que les corps emploieront à faire leur révolution entière ou à parcourir des arcs semblables, seront en raison inverse de la triplée des distances.

13°. Ces différentes lois sont aisées à déduire de la formule que nous avons donnée dans l'art. 1. pour la comparaison des forces centrales entr'elles. Or pour comparer les forces centrales sur des courbes autres que des cercles, il faut prendre au lieu des rayons des cercles, les rayons de la développée de ces courbes qui changent à chaque point, et qu'on trouve par des méthodes géométriques : d'où l'on voit que quand un corps décrit une courbe autre qu'un cercle, la valeur de la force centrale change à chaque instant ; au lieu qu'elle est toujours la même quand le corps décrit un cercle. Il faudra de plus diviser la quantité trouvée par le rapport du sinus total au cosinus de l'angle que la direction de la force centrale fait avec la tangente.

14°. Si un corps tend à se mouvoir suivant A D (fig. 25.), et qu'il soit en même temps sollicité par une force centripete vers un point fixe C, placé dans le même plan, il décrira alors une courbe dont la concavité sera tournée vers C, et dont les différentes aires comprises entre deux rayons quelconques A C et C B, seront proportionnels aux temps employés à parcourir ces aires, c'est-à-dire à parvenir de l'extrémité d'un de ces rayons à l'extrémité de l'autre. Car sans la force centrale qui pousse suivant B F, le corps parcourait dans des temps égaux B D = A B : mais à cause de la force centrale, il décrira la diagonale B E du parallelogramme F B D E dans le même temps qu'il a décrit A B. Or le triangle C B A = C B D, à cause de B D = A B ; et à cause des parallèles D E, F B, on a C B E = C B D. Donc C B E = C A B. Donc, etc.

15°. Quelque différentes que soient des forces centrales dans des cercles, on pourra toujours les comparer ensemble : car elles seront toujours en raison composée de celle des quantités de matière que contiennent les mobiles, de celles de leur distance au centre, et enfin de l'inverse de la doublée des temps périodiques. Si l'on multiplie donc la quantité de matière de chaque mobîle par sa distance du centre, et qu'on divise le produit par le carré du temps périodique, les quotiens qui résulteront de ces opérations seront entr'eux dans la raison des forces centrales : c'est une suite de l'article 1.

16°. Si les quantités de matières sont égales, il faudra diviser les distances par les carrés des temps périodiques, pour déterminer le rapport des forces centrales.

17°. Lorsque la force par laquelle un corps est sollicité vers un point, n'est pas par-tout la même, mais qu'elle augmente ou diminue à proportion de la distance du centre ; cette nouvelle condition fait décrire alors au mobîle différentes courbes plus ou moins composées. Si la force décroit en raison inverse des carrés des distances à ce point, le mobîle décrira alors une ellipse, qui est une courbe ovale, dans laquelle se trouvent deux points qu'on nomme foyers, dont l'un est alors occupé par le point T, vers lequel se dirige la force dont nous parlons ; de façon qu'à chaque révolution le corps s'approche une fois de ce point, et s'en éloigne une fais. Le cercle appartient aussi à cette espèce de courbe ; de sorte que dans ce cas le mobîle peut aussi décrire un cercle. Le mobîle peut aussi, en lui supposant une plus grande vitesse, décrire les deux autres sections coniques, la parabole, et l'hyperbole ; lesquelles ne retournent point sur elles-mêmes. Si la force croit en même temps que la distance, et en raison de la distance même, le corps décrira encore une ellipse : mais le point vers lequel se dirigera la force, sera alors le centre de l'ellipse, et le mobîle à chaque révolution s'approchera deux fois et s'éloignera deux fois de ce point. Il peut arriver encore en ce cas, que le corps se meuve dans un cercle. Voyez ORBITE, PLANETE, TRAJECTOIRE et PROJECTILE. Voyez aussi les principes mathém. de M. Newton, liv. I. et les éléments de mécan. de Wolf.

Les courbes peuvent être considérées, ou comme courbes rigoureuses, ou comme polygones infinis ; or l'expression de la force centrale est différente dans les deux cas : ce paradoxe singulier sera expliqué à l'article COURBE.

Regle centrale ; c'est une règle ou une méthode qui a été découverte par Thomas Baker, géomètre anglais ; au moyen de laquelle on trouve le centre et le rayon du cercle qui peut compter une parabole donnée dans des points, dont les abscisses représentent les racines réelles d'une équation du troisième ou du quatrième degré qu'on se propose de construire. Voyez CONSTRUCTION.

La règle centrale est surtout fondée sur cette propriété de la parabole ; que si on tire dans cette courbe une perpendiculaire à un diamètre quelconque, le rectangle formé des segments de cette ligne, est égal au rectangle fait de la portion correspondante du diamètre, et du paramètre de l'axe.

La règle centrale est préférable, selon Baker, aux méthodes de Descartes pour construire les équations, en ce que dans cette dernière on a besoin de préparer l'équation, en lui ôtant le second terme ; au lieu que dans celle de Baker on n'a point cet embarras, puisqu'elle donne le moyen de construire, par l'intersection d'un cercle et d'une parabole, toute équation qui ne passe pas le quatrième degré, sans en faire évanouir ni changer aucun terme. Voyez Transactions philosophiq. n °. 157. Mais il est très-facile, en suivant l'esprit de la méthode de Descartes, de construire par le moyen du cercle et de la parabole, toutes les équations du troisième et du quatrième degré, sans en faire évanouir le second terme. Voyez la solution de ce problème dans l'article 386. des sections coniques de M. de l'Hôpital. (O)

CENTRAL